# 1 静态分析概述

# 1.1 静态分析的基本概念

定义1.1

静态分析（Static Analysis） 是指在实际运行程序 $P$ 之前，通过分析静态程序 $P$ 本身来推测程序的行为，并判断程序是否满足某些特定的 性质（Property） $Q$ 。

我们会关心的程序性质可能有：

程序P是否会产生私有信息泄漏（Private Information Leak），或者说是否存在访问控制漏洞（Access Control Vulnerability）；
程序P是否有空指针的解引用(Null Pointer Dereference)操作，更一般的，是否会发生不可修复的运行时错误（Runtime Error）；
程序P中的类型转换（Type Cast）是否都是安全的；
程序P中是否存在可能无法满足的断言（Assertion Error）；
程序P中是否存在死代码（Dead Code, 即控制流在任何情况下都无法到达的代码）；

有些可惜的是，静态分析并不能对于我们上面关心的问题给出一个确切的答案。

定理1.1 Rice定理（Rice Theorem）

对于使用 递归可枚举（Recursively Enumerable） 的语言描述的程序，其任何 非平凡（Non-trivial） 的性质都是无法完美确定的。

在这个定理中，有几个字眼需要我们稍微关注一下：

关于递归可枚举，其含义是存在某个计算函数（可以是图灵机），能够将这种语言中的所有合法字符串枚举出来。这个概念有些抽象，不必深究，暂时只需要知道，目前我们所能想到的所有的编程语言都是递归可枚举语言。
关于非平凡，我们认为，如果一种性质是所有的程序都满足的或者都不满足的，那么这种性质就是平凡的，除此之外的性质都是非平凡的。其实和程序运行时的行为相关的，让我们感兴趣的性质，基本都是非平凡的性质。

# 1.2 静态分析的类型

# 1.2.1 完美的静态分析

定义1.2

如果一个静态分析 $S$ 能够对于程序 $P$ 的某个非平凡性质 $Q$ 给出确切的答案，我们就称 $S$ 是 $P$ 关于 $Q$ 的 完美静态分析（Perfect Static Analysis） 。我们定义程序P的关于Q的真实行为为 真相（Truth） ，那么完美静态分析有两层含义：

完全性（Soundness）：真相一定包含在 $S$ 给出的答案中；
正确性（Completeness）： $S$ 给出的答案一定包含在真相中；

记这个静态分析程序给出的答案集合 $A$ ，真相集合为 $T$ ，则完美的静态分析满足：

T \subseteq A \wedge A \subseteq T \Leftrightarrow A = T

其中， $T \subseteq A$ 体现了完全性， $A \subseteq T$ 体现了正确性。

简单理解，一个完美的静态分析给出的答案应当既是对的，也是全的。

但是Rice定理告诉我们，不存在完美的静态分析，那么静态分析是否就没用了呢？并不是，有用和完美之间，往往是有着一片广阔的空间的。

# 1.2.2 妥协的静态分析

因为完美的静态分析并不存在，所以我们通常需要做一些妥协，也就是在 $T \subseteq A$ 和 $A\subseteq T$ 中只尽力满足其中一个条件，妥协另一个条件。

于是，我们得到了两种妥协后的静态分析类型。

定义1.3

记程序 $P$ 的关于性质 $Q$ 的静态分析S为 Sound 的静态分析（Sound Static Analysis） ，当且仅当 $S$ 给出的答案集合 $A$ 和 $P$ 关于 $Q$ 的真相集合 $T$ 之间满足 $T \subseteq A$ ，这种分析策略也称作 过近似（Over-approximation） 。

定义1.4

记程序 $P$ 的关于性质 $Q$ 的静态分析 $S$ 为 Complete 的静态分析（Complete Static Analysis） ，当且仅当 $S$ 给出的答案集合 $A$ 和 $P$ 关于 $Q$ 的真相集合 $T$ 之间满足 $A \subseteq T$ ，这种分析策略也称作 欠近似（Under-approximation） 。

其中，

Sound 的静态分析保证了完全性，妥协了正确性，会过近似（Overapproximate）程序的行为，因此会出现假积极（False Positive）的现象，即判定为积极，但实际是消极的。反映在现实场景中即为误报问题。

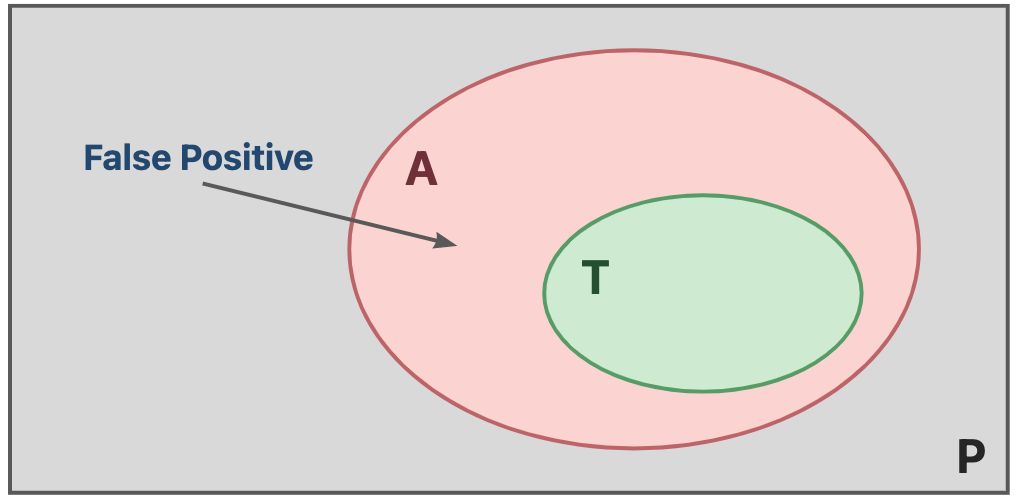
false-positive

在继续推进之前，我们先解释一下积极和消极的含义，对于客观世界来说， $T$ 是积极的， $\overline T$ 是消极的，从 $S$ 的视角来看， $A$ 是积极的， $\overline A$ 是消极的。

所谓假积极，就是 $S$ 认为的积极其实在客观世界中是消极。类似的，假消极也就可以理解了。

这里，借用之前的形式化语言，我们其实可以明确的定义出在静态分析中的 False Positive ：

定义1.5

记程序 $P$ 的关于性质 $Q$ 的静态分析S有 假积极（False Positive） 问题，当且仅当 $S$ 给出的答案 $A$ 和 $P$ 关于 $Q$ 的真相T满足如下关系：

\exists a \in A, a\notin T

其中， $a$ 称为一个 假积极实例（False Positive Instance） ，其实是一个 消极实例（Negative Instance） 。

Complete 的静态分析保证了正确性，妥协了完全性，会欠近似（Underapproximate）程序的行为，因此会出现假消极（False Negative）现象，即判定为消极（在 $\overline A$ 中），但实际是积极（在 $T$ 中）。反映在现实场景中即为漏报问题。

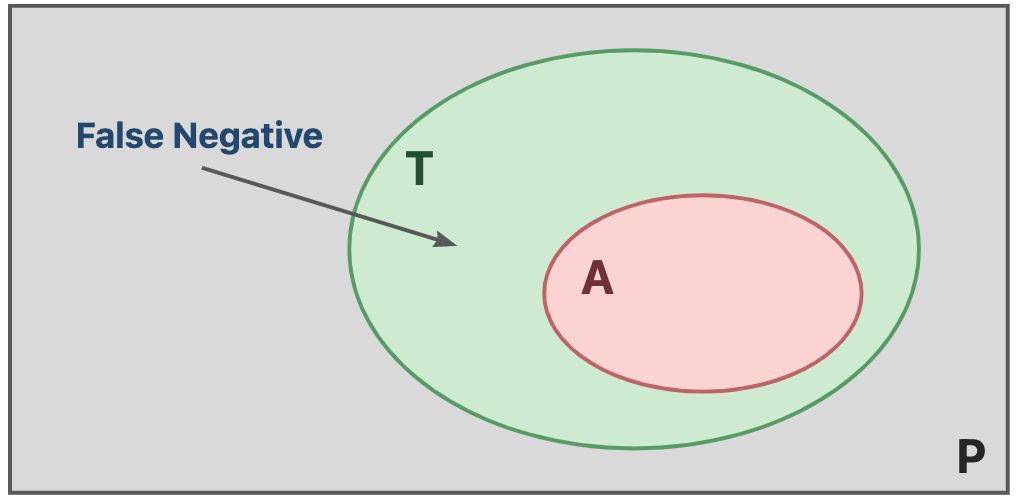
false-negative

和定义1.5类似，我们可以形式化的定义出False Negative：

定义1.6

记程序 $P$ 的关于性质 $Q$ 的静态分析 $S$ 有 假消极（False Negative） 问题，当且仅当 $S$ 给出的答案 $A$ 和 $P$ 关于 $Q$ 的真相 $T$ 满足如下关系：

\exists a \notin A, a\in T

其中， $a$ 称为一个 假消极实例（False Negative Instance） ，其实是一个 积极实例（Positive Instance） 。

# 1.2.3 现实世界中有用的静态分析

大多数的静态分析会妥协正确性，保证完全性，即 Sound 的静态分析居多，这样的静态分析虽然不是完美的，但是有用的。以 debug 为例，在实际的开发过程中，Sound 的静态分析可以帮助我们有效的缩小 debug 的范围，我们最多只需要暴力排查掉所有的假积极实例（False Positive Instance）就可以了。

由于假积极实例 $a \in A$ ，所以这个人工排查 $a$ 的代价仍然是可控的，假设暴力排查一个程序点是否为 bug 的平均代价是常数项时间，则排查假积极的代价在 $O(|A|)$ 以内。除非该 Sound 的分析极其不精确，导致 $|A|$ 特别的大，否则 $O(|A|)$ 是一个可以接受的代价，有一点错误的 Warning 问题不大。

但是，Complete 的静态分析做不到这一点，它不能够帮助我们有效缩小 debug 的范围。因为假消极实例（False Negative Instance） $a \notin A$ ，所以 $a$ 的范围是 $P - A$ 。这里注意的是，虽然假消极的理论范围是 $T - A$ ，但因为我们并不知道 $T$ 是什么，所以只能从 $P - A$ 中排查。而 $P - A$ 往往是比 $A$ 大得多的，因此排查假消极的代价是很大的。

除非存在某个 Complete 的静态分析 $S$ ，能够做到 $A$ 接近于 $P$ （这里的 $P$ 理解为整个程序的全集），这样 $P - A$ 会比较小，从而排查假消极的代价就小了。但是 $A \subseteq T \subseteq P$ ，如果要做到让 $A$ 接近于 $P$ ，我们就需要一个 $T$ 接近于 $P$ 的前提条件，因为 Complete 分析下 $A$ 不会超过 $T$ 。

换言之，为了让排除假消极变得容易，需要程序 $P$ 本身就十分符合性质 $Q$ 。但是，如果静态分析 $S$ 对于程序 $P$ 本身提出了 $P$ 接近于 $T$ 的要求，那么我们还要静态分析干嘛呢？

我们使用静态分析的原因就是我们做不到写出非常符合 $Q$ 的 $P$ （如果 $Q$ 是一个优良的性质）或者我们根本不会去分析非常符合 $Q$ 的 $P$ （如果 $Q$ 是一个糟糕的性质，那么非常符合 $Q$ 的 $P$ 就是一个非常糟糕的程序，我们需要分析的往往是普通的程序），也就是 $P$ 本身达不到我们的期待，所以才需要静态分析来帮助改进 $P$ 。

上面一段逻辑分析好像有点绕，不知道读者能不能理解逻辑（含义应该是好理解的，只是逻辑有点绕）。

下面我们再看一个 Sound 的静态分析的例子：

if input then
    x = 1;
else
    x = 0;
output x;

1
2
3
4
5

我们可以有两种 Sound 的静态分析：

当 input 为 true ，x 为 1 ，当 input 为 false ， x 为 0 ；
x 为 0 或 1

这两种都保证了完全性，不过前者更精确，代价也更高；后者不那么精确，但相应的，代价也会更低一点。我们需要根据实际情况选择使用哪一种，也就是说在精度和速度之间做一个权衡。

基于上述所有的内容，我们可以对现实世界（Real World）中的静态分析做一个总结：

结论1.1

现实中的静态分析（Real-World Static Analysis） 需要保证（或者尽可能保证）完全性（Soundness） ，并在 速度（Speed） 和 精度（Precision） 之间做出一个合适的 权衡（Trade-off） 。

# 1.3 抽象

结论1.2

如果用两个词概括静态分析，可以是 抽象（Abstraction） 和 过近似（Overapproximation） 。

其中，过近似已经阐释的很清楚了（一个式子总结就是 $T \subseteq A$ ），下面我们来看一下抽象。

# 1.3.1 抽象的概念

当我们考虑程序P的性质 $Q$ 时，程序 $P$ 中的各种值，我们或许不一定非得事无巨细。比如说，当我们考虑除零错误（Zero Division Error）的时候，对于某个值，我们只需要判定其是否为 $0$ 即可，至于它具体是多大，我们其实不关心，因为它和我们要研究的性质 $Q$ 没有直接关联。

这种将 $P$ 中的值的，和我们需要研究的性质 $Q$ 相关的性质提取出来，从而忽略其他细节的过程，就是一个抽象的过程。我们可以将这个过程形式化的定义出来：

定义1.7

对于程序 $P$ 的某个 具体值集（Concrete Domain） $D_C$ ，静态分析 $S$ 基于要研究的性质 $Q$ 设计一个 抽象值集（Abstract Domain） $D_A$ （一般 $|D_A| < |D_C|$ ，因为这样的设计才有简化问题的意义），并建立映射关系 $f_{D_C \to D_A}$ （ $f_1 \subseteq D_C \times D_A$ ），这个过程称之为 $S$ 对 $P$ 关于 $Q$ 的 抽象（Abstraction） 过程。

其中， $D_A$ 中通常有两个特殊的值： $\top$ 表示 未确定（Unknown） 值， $\bot$ 表示 未定义（Undefined） 值，即通常 $\top \in D_A \wedge \bot \in D_A$ ，并且通常 $\top$ 和 $\bot$ 会是程序中的表达式的值，因此我们还需要定义基于 $D_A$ 的运算（定义1.8）来理解 $\top$ 和 $\bot$ 。

当我们定义了 $D_A$ 和 $f_{D_C\to D_A}$ 之后，与 $D_C$ 有关的表达式的抽象值也应当能够随之确定，为此，我们还需要定义状态转移函数。

定义1.8

基于定义1.7，记 $f_1 = f_{D_C \to D_A}$ 考虑程序 $P$ 关于 $D_C$ 的二元操作集 $Op$ ，我们可以建立映射 $f_2 = f_{Op \times D_A \times D_A \to D_A}$ （ $f_2 \subseteq Op \times D_A \times D_A\times D_A$ ），这样，我们就可以将所有 $D_c$ 相关的表达式的值通过 $f_2 \circ f_1$ 也映射到 $D_A$ 。其中 $f_1$ 称为 状态函数（State Function） ， $f_2$ 称为 转移函数（Transfer Function） 。

由此可见，状态函数定义了我们如何将具体值转化为抽象值，转移函数定义了我们如何基于抽象值去 解析（Evaluate） 表达式。

这里需要额外说明一下的事，我们定义了 $Op$ 为二元操作集，其原因是下一讲中，我们会学习 三地址码（Three-Address Code, 3AC） ，从而我们能够发现二元操作集表达能力的完备性，因此这里可以将 $Op$ 定义为二元操作。

# 1.3.2 一个静态分析的例子

举一个例子，假如我们研究程序中变量的正负性，则我们可以设计 $D_A = \{+, -, 0, \top, \bot\}$ ，定义 $f_1 = f_{D_C\to D_A}$ ：

\forall x \in D_C, f_1(x)= \begin{cases} +, if\ x > 0\\ 0, if\ x = 0\\ -, if\ x < 0\\ \end{cases}

再定义 $f_2 = f_{Op\times D_A\times D_A \to D_A}$ 如下：

f_2 = \{(+, +, +, +), (+, -, -, -), (+, +, -, \top), (+, 0, 0, 0),

(/, +, +, +), (/, -, -, +), (/, \top, 0, \bot), (/, +, -, -), ......\}

基于此：

如果我们分析出某个数组的下标为 $\top$ ，那么我们就可以过近似地（Overapproximately）认为这个地方很可能会发生数组越界错误（Index Out of Bound Exception）；
如果我们分析出某个数组的下标为 $-$ ，那么我们就可以欠近似地（Underapproximately）认为这个地方一定会发生数组越界错误（Index Out of Bound Exception）；
如果我们分析出某个地方出现了值 $\bot$ ，我们可以欠近似地确认，这个地方一定会发生除 0 错误（Zero-Division Error）
如果我们分析出某个地方的分母为 $\top$ ，那么我们也可以过近似地认为这个地方会发生除 0 错误。

于是，我们发现，抽象确实能够帮助我们分析问题，得出一些结论。其中，我们能够直观的感受到：

第2条和第3条结论是具有 正确性（Completeness） 但不是完全的；
第4条结论具有 完全性（Soundness） 但并不一定是正确的；
第1条结论既没有完全性，也没有正确性，但是，它能够囊括一部分的真相。

于是，上述的静态分析S总体上是妥协了正确性（因为基于1.2.3中尽可能完全的原则，最终我们的答案应该会取并集——过近似 Overapproximate），接近完全（Close To Soundness）（其实也没有达到完全）的一种静态分析。

# 1.3.3 Sound 的分析和过近似

再看一个例子，体会一下 Sound 的，过近似的分析原则：

x = 1;
if input then
    y = 10;
else
    y = -1;
z = x + y;

1
2
3
4
5
6

我们会发现，在进入 2-5 行的条件语句的时候， $y$ 的值可能为 $10$ ，也可能为 $-1$ ，于是，我们最终会认为y的抽象值为 $\top$ ，最终 $z$ 的抽象值也就为 $\top$ ，这样，我们的分析就是尽可能全面的，虽然它并不精确。

# 1.4 自检问题

静态分析（Static Analysis）和动态测试（Dynamic Testing）的区别是什么？
完全性（Soundness）、正确性（Completeness）、假积极（False Positives）和假消极（False Negatives）分别是什么含义？
为什么静态分析通常需要尽可能保证完全性？
如何理解抽象（Abstraction）和过近似（Over-Approximation）？