2 程序的中间表示

2.1 编译器和静态分析器

2.1.1 编程语言的各个层次

我们编写的源文件本质上是一个ASCII码字符串文件，它最终会被转化为二进制比特流以供CPU处理。一般的，需要编译的静态类型语言，其源代码向机器码转化的过程大致如下：

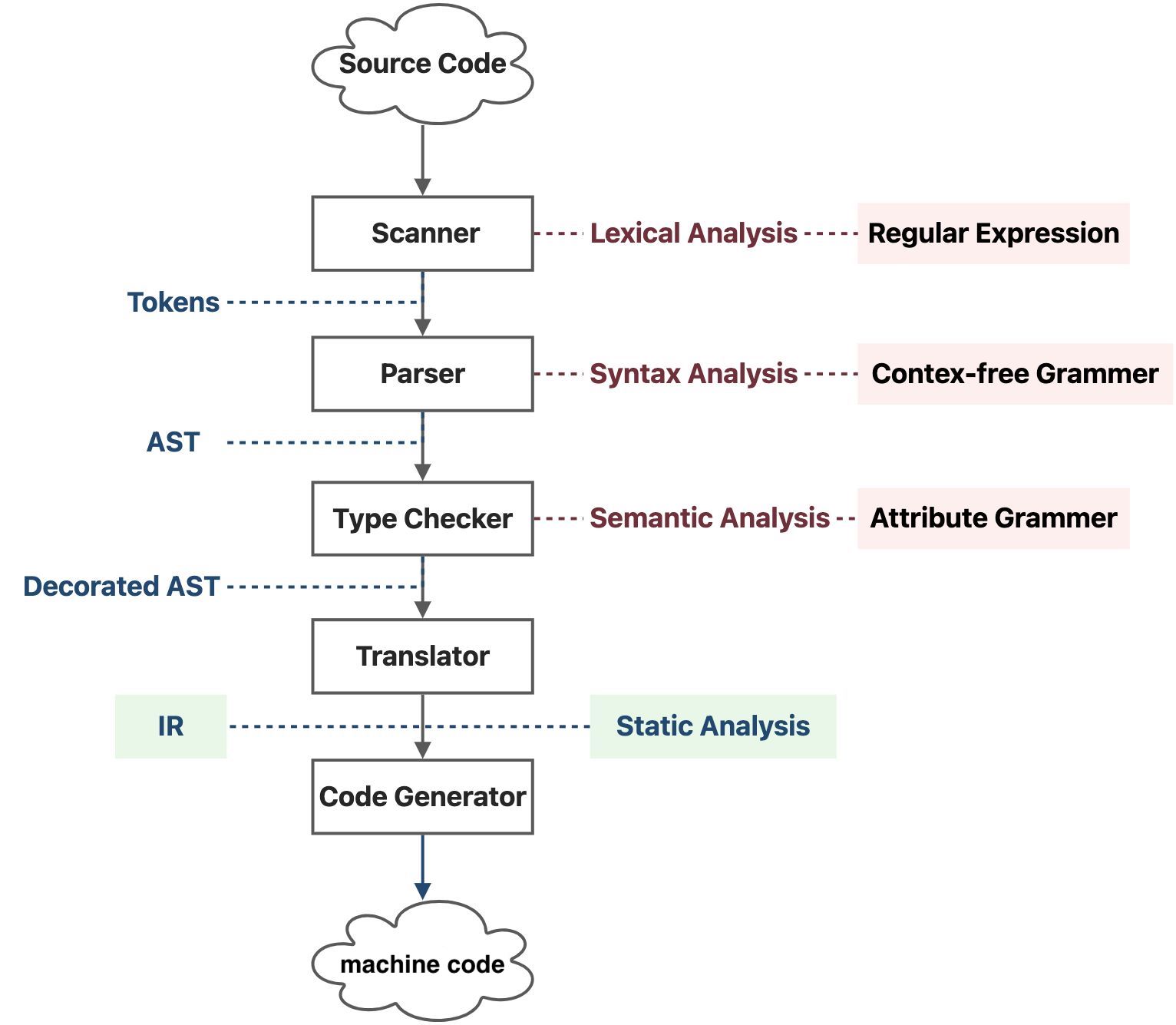
• 扫描器（Scanner） 扫描源代码，进行词法分析（Lexical Analysis）,词法分析会用到正则表达式（Regular Expression），词法分析后的结果为一个标记（Token）串。

• 解析器（Parser） 遍历标记串，进行语法分析（Syntax Analysis），这里的语法分析分析的是上下文无关的语法（Context Free Grammer），解析器的内部应该是实现了一个有限状态机，用于识别和分析每个语法块格式的正确性，语法分析的结果为一棵抽象语法树（Abstract Syntax Tree, AST）。

• 类型检查器（Type Checker） 会遍历抽象语法树，进行语义分析（Semantic Analysis），不过编译器的语意分析是简单的，主要是分析属性语法（Attribute Grammer），比如说变量类型，并适当调整一下语法树。语义分析的结果我们称之为装饰过的抽象语法树（Decorated AST）。

• 翻译器（Translator） 会将抽象语法树翻译成中间表示（Intermediate Representation, IR），IR 的出现解耦了编译器的机器相关（Machine Dependent）部分和机器无关（Machine Independent）部分，上述几个层次在不同架构的机器上面是可以几乎不加改动地复用的。

• 机器码生成器（Code Generator） 会将 IR 转化成物理 CPU 能够直接执行的比特序列，这个过程是机器相关的。

而静态分析通常发生在 IR 这一层次，这也是我们作代码的机器无关优化的一个层次，同时也是即将生成目标代码的一个层次。不过适合代码生成的 IR 和适合分析的 IR 不一定是同一个，一般来讲抽象层次更低一些的 IR 对于代码生成会更加友好，抽象层次稍高一些的 IR 对于静态分析会更加友好一些。

2.1.2 抽象语法树和中间表示的对比

考虑下面一小段代码：

do i = i + 1; while (a[i] < v);

这段代码的AST和IR分别为：

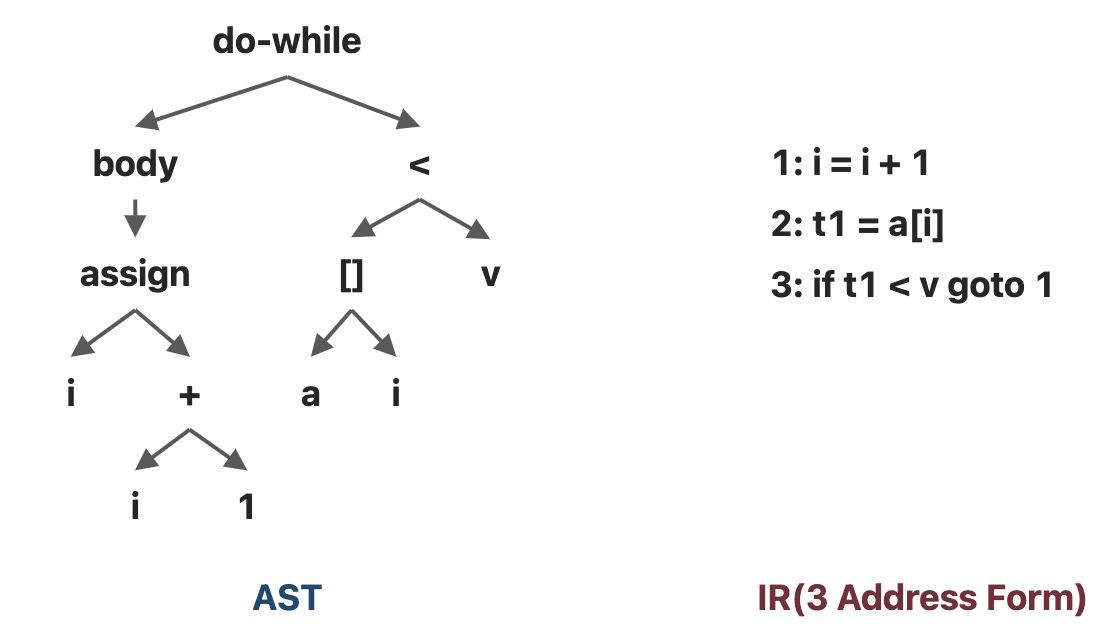
AST	IR
层次更高，和语法结构更接近	低层次，和机器代码相接近
通常是依赖于具体的语言类的	通常和具体的语言无关，主要和运行语言的机器（物理机或虚拟机）有关
适合快速的类型检查	简单通用
缺少和程序控制流相关的信息	包含程序的控制流信息
	通常作为静态分析的基础

定义2.1

我们将形如 $f(a_1, a_2, ..., a_n)$ 的指令称为 $n$ 地址码（N-Address Code），其中，每一个 $a_i$ 是一个地址，既可以通过 $a_i$ 传入数据，也可以通过 $a_i$ 传出数据， $f$ 是从地址到语句的一个映射，其返回值是某个语句 $s$ ， $s$ 中最多包含输入的 $n$ 个地址。这里，我们定义某编程语言 $L$ 的语句 $s$ 是 $L$ 的操作符、关键字和地址的组合。

我们后续使用的是 3 地址码形式的 IR ，一方面是因为一些历史传统，一些经典的分析算法是以 3 地址码作为 IR 的所以这种表示方法就一直沿用着；另一方面是因为它表示上更加简洁方便且表达能力完备。

但是这里需要注意一下的是，IR 不一定非得是 3 地址码， IR 的含义只是“中间表示”而已，只要方便达成你的目的即可，AST，DAG（Directed Acyclic Graph）也是会使用到的 IR 形式，不过最常用的其实还是 3 地址码。

2.1.3 3地址码

下面我们具体来看一下3地址码。3地址码中的地址可能有如下的几种类型：

• 名字（Name），包括

  • 变量（Variable）

  • 标签（Label）

    • 用于指示程序位置，方便跳转指令的书写

• 字面常量（Literal Constant）

• 编译器生成的临时量（Compiler-Generated Temporary）

每一种指令都有其对应的 3 地址码形式，一些常见的 3 地址码形式如下：

x = y bop z
x = uop y
x = y
goto L
if x goto L
if x rop y goto L

其中：

• x, y, z是变量的地址；

• bop 是双目操作符（Binary Operator），可以是算数运算符，也可以是逻辑运算符；

• uop 是单目操作符（Unary Operator），可能是取负、按位取反或者类型转换；

• L 是标签（Label），是标记程序位置的助记符，本质上还是地址；

• rop 是关系运算符（Relational Operator），运算结果一般为布尔值。

• goto 是无条件跳转， if... goto 是条件跳转。

这里对于一些常见场景的三地址码结构，最好有一个直观的感知，这些场景包括循环结构、分支结构、方法调用和类。其实，如果有一定的汇编基础，对于三地址码的阅读和汇编差不多，甚至比汇编更简单。

这里需要注意一下的是，无论是三地址码还是汇编，其指令类型不取决于具体的语言，而取决于运行这个语言的机器的指令集体系结构（Instruction Set Architecture，ISA），Java虚拟机有自己的指令集体系结构，x86的CPU、Arm的CPU，RISCV的CPU也都有着自己的体系结构。这个运行语言的机器可以是物理机（比如说CPU），也可以是虚拟机（比如说JVM-Java Virtual Machine）。

2.1.4 静态单赋值表示

静态单赋值（Static Single Assignment，SSA） 是另一种IR的形式，它和3AC的区别是，在每次赋值的时候都会创建一个新的变量，也就是说，在SSA中，每个变量（包括原始变量和新创建的变量）都只有唯一的一次定义。

当控制流汇合（Merge）的时候，我们会用一个特殊的操作符表示汇和后的定义：

$x_3 = \phi(x_1, x_2) = \begin{cases} x_1, & \text{if true}\\ x_2, & \text{otherwise} \end{cases}$

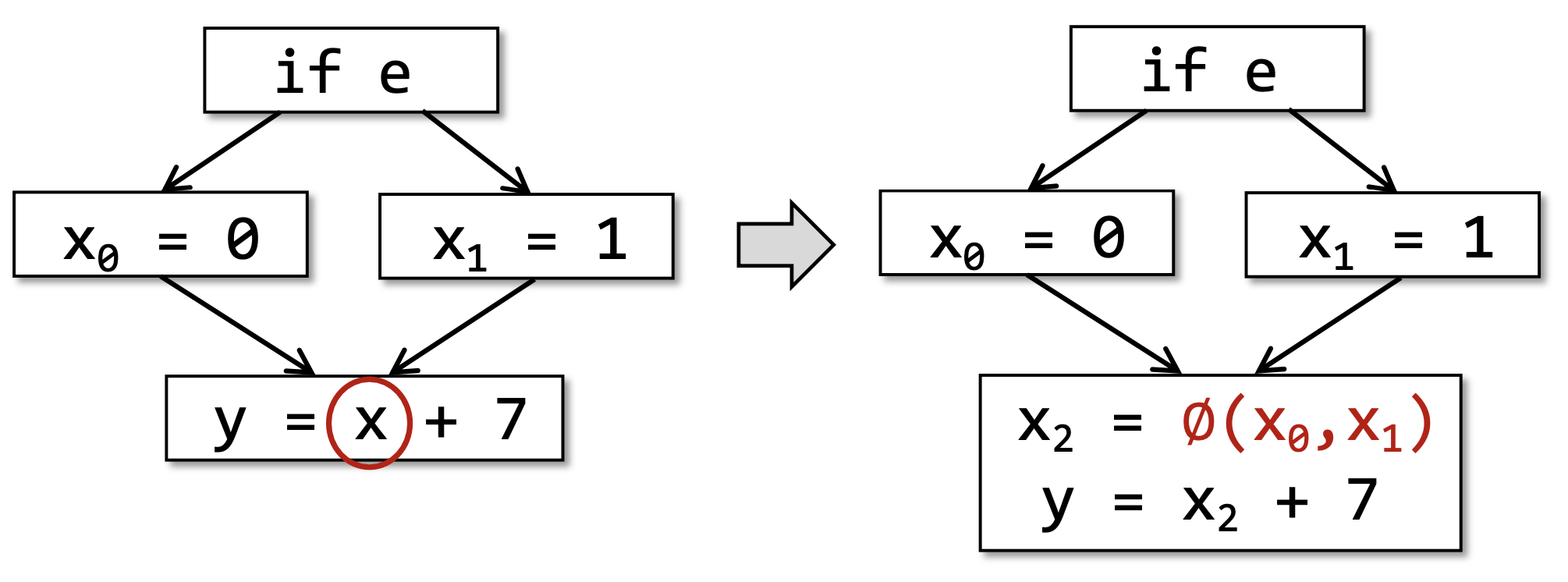
关于SSA，我们只要简单了解一下定义和优缺点就可以了，之后还是用3AC比较多。

• 优点：

  • 控制流的信息间接地被包含在了独特的变量名之中

    • 当我们做一些对控制流敏感的分析的时候，这些信息可能会有帮助

  • 定义和使用的关系明确

• 缺点：

  • 可能会引入过多的变量名和$\phi$函数

  • 被翻译成机器码的时候效率低，因为有太多对于程序执行来说不必要的赋值

2.2 控制流分析

控制流分析（Control Flow Analysis, CFA） 通常是指构建 控制流图（Control Flow Graph，CFG） 的过程。

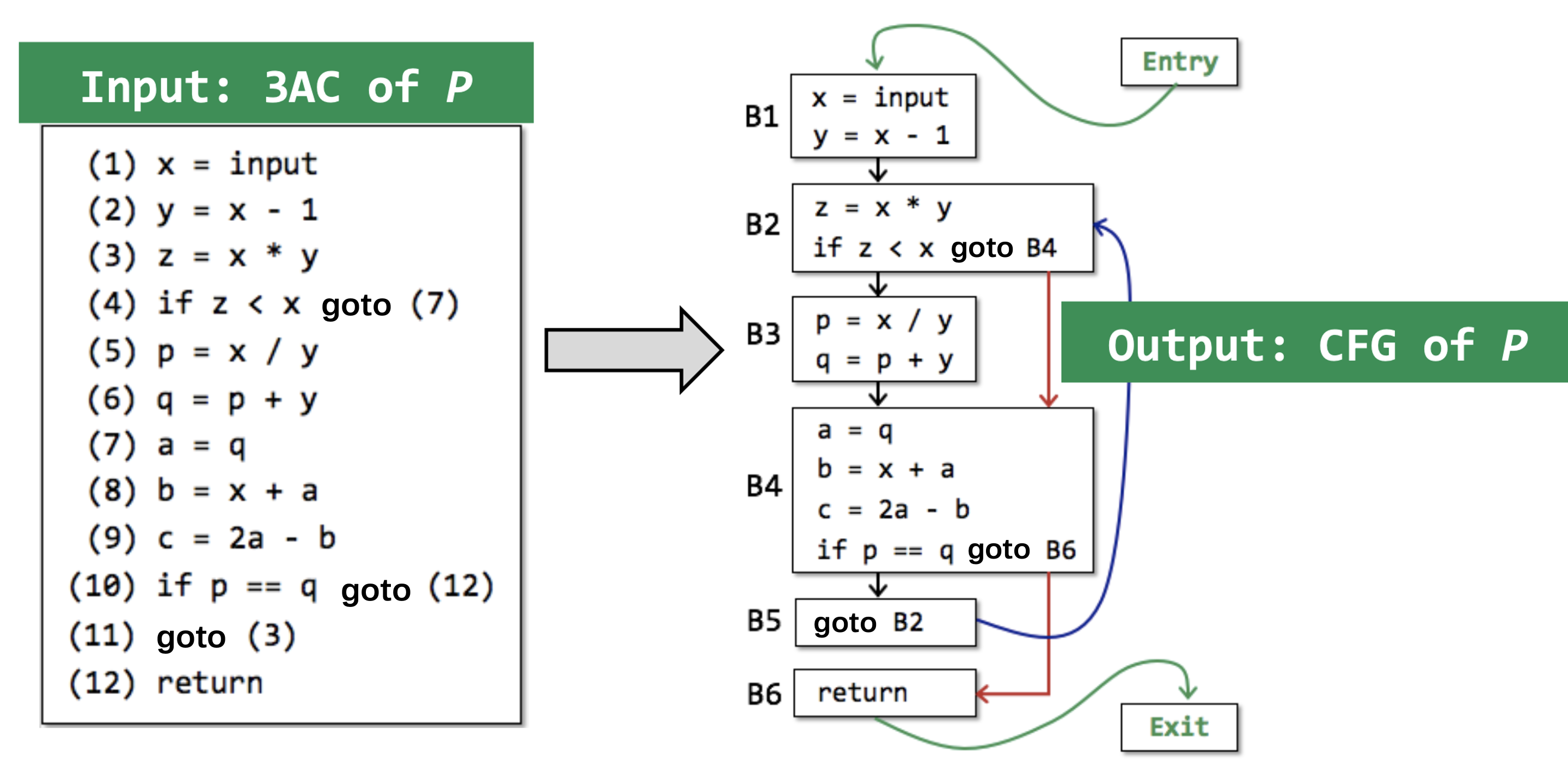
2.2.1 基块

CFG是我们进行静态分析的基础，控制流图中的结点可以是一个指令，也可以是一个基块（Basic Block）。

定义2.2

记一个程序 $P$ 在IR表示下 的指令序列为 $P = \{a_1, a_2, ..., a_n\}$ ，这里 $P$ 是一个有序集。我们定义

• $IN_i = \{a_j | next(a_j) = a_i\}$ ，其中 $next(a_j)$ 表示控制流中 $a_j$ 的下一条指令；
• $OUT_i = \{a_j | prev(a_j) = a_i\}$ ，其中 $prev(a_j)$ 表示 $a_j$ 的上一条指令。

如果连续的指令序列 $a_p, a_{p + 1}, a_{p + 2}, ... a_q$ 的满足如下性质：

$\forall i \in [p + 1, q], IN_i = \{a_{i - 1}\} \wedge \forall i\in [p, q - 1], OUT_i = \{a_{i + 1}\}$

并且 $a_{p - 1}, a_p, ... ,a_{q - 1}, a_q$ 和 $a_p, a_{p + 1}, ... a_{q}, a_{q + 1}$ 都不满足上述性质，则称 $\{a_p, a_{p + 1}, ..., a_q\}$ 为基块（Basic Block）。

简单理解，基块就是满足如下性质的最长指令序列：

• 程序的控制流只能从首指令进入

• 程序的控制流只能从尾指令流出

于是我们可以直观的感受到，跳转指令会将一个完整的程序块切割为几个基块，如果我们能够把基块的分隔点找出来，那么整个程序P就可以被我们转化成许多的基块了。

定义2.3

对于IR表示下的程序 $P = \{a_1, a_2, ..., a_n\}$ ，考虑某个基块 $B = \{a_p, a_{p + 1}, ..., a_{q - 1}, a_q\}$ ，我们称 $a_p$ 为 $P$ 的基块 $B$ 的领导者（Leader）。

定理2.1

考虑程序 $P = \{a_1, a_2, ..., a_n\}$ 中所有的领导者组成的集合为 $L$ ，则

$L = \{a_1\} \cup \{a_j | \exists a_i, type(a_i) = jump \wedge target(a_i) = a_j\} \cup \{a_{i + 1} | type(a_i) = jump\}$

其中， $type(a_i)$ 表示指令 $a_i$ 的类型，jump类型是跳转指令，包括条件跳转（Conditional Jump） 和 无条件跳转（Unconditional Jump）， $target(a_i)$ 仅用于 $a_i$ 是跳转指令的时候，表示 $a_i$ 的目标指令。

简单理解，一个基块的领导者就是这个基块的首指令，整个程序中的领导者有如下3种：

• 整个程序的首指令；

• 跳转指令（包括条件跳转和无条件跳转）的目标指令；

• 跳转指令（包括条件跳转和无条件跳转）紧接着的下一条指令。

定理2.2

考虑程序 $P = \{a_1, a_2, ..., a_n\}$ 中所有的领导者组成的集合为 $L$ ，则有

$a_p \in L \wedge a_{q + 1} \in L \wedge \forall a_i(i \in [p + 1, q]), a_i \notin L \Leftrightarrow \{a_p, a_{p + 1}, ..., a_{q - 1}, a_q\}\ is\ basic\ block$

简单理解，从一个Leader到紧接着的下一个Leader之前的所有指令组成了一个基块。

基于定理2.1和定理2.2，我们可以设计出一个寻找基块的算法：

算法2.1 基于中间表示的基块构建算法

算法的时间复杂度为 $O(n)$ 。

在实际实现过程中，由于保证前$i$个指令的Leader数量不超过$i$个，因此在第二重循环中一定保证$k\le i$恒成立。因此，IsLeader和L可以合并使用，上述伪代码出于方便理解考量下未能如此实现。当然空间复杂度一样为 $O(n)$ 。

2.2.2 控制流图

定义2.4

记程序 $P$ 的基块组成了集合 $B = \{b_1, b_2, ..., b_k\}$ ，考虑图 $CFG_0 = (B, E_0)$ ，其中 $E_0\subseteq B\times B$ ，满足

$E_0 = \{(b_i, b_j) | (type(last(b_i)) = jump \wedge target(last(b_i)) = first(b_j)) \vee$

$(next(last(b_i)) = first(b_j)\wedge type(last(b_i))\ne unconditional\ jump) \}$

其中， $first(b_i)$ 表示基块 $b_i$ 的首指令（也就是Leader）， $last(b_i)$ 表示基块 $b_i$ 的尾指令， $next(x)$ 表示指令 $x$ 紧随其后的指令。其余记号含义同定理2.1。

如果 $(b_i, b_j)\in E_0$ ，我们称 $b_i$ 是 $b_j$ 的 前驱（Predecessor） ， $b_j$ 是 $b_i$ 的 后继（Successor） 。

• 对于图 $CFG_0$ 中所有入度为0的点（一般只有一个），考虑虚拟结点 入口（Entry） ，所有的 入度（In Degree） 为0的点都是Entry的后继；

• 对于图 $CFG_0$ 中所有出度为0的点（可能不止一个），考虑虚拟结点 出口（Exit） ，所有的 出度（Out Degree） 为0的点都是Exit的前驱。

记 $E_1 = \{(Entry, b) | b \in B \wedge inDegree(b) = 0\},E_2 = \{(b, Exit) | b \in B \wedge outDegree(b) = 0\}$ 则我们可以定义 控制流图（Control Flow Graph） 为 $CFG = (V, E)$ ，其中

$V = B \cup \{Entry, Exit\}, E = E_0 \cup E_1\cup E_2$

简单理解上述定义，程序控制流的产生来源于两个地方：

• 天然的顺序执行

  • 这是计算系统天然存在的一种控制流

• 跳转指令

  • 这是人为设计添加的一种控制流

基于上述定义，我们可以得到构建CFG的算法：

算法2.2 基于基块的控制流图构建算法

这个算法的时间复杂度为 $O(k)$ 。

其实，从计算机硬件的角度分析，程序的控制流体现在 程序计数器（Program Counter, PC） 的增减上。 每一种架构的CPU都会有PC，比如说x86的CPU用EIP（Extended Instruction Pointer）作为PC，RISCV的CPU用IR（Instruction Registor）作为PC，JVM应该也应该有对应的PC存在。

2.3 自检问题

1. 编译器（Compiler）和静态分析器（Static Analyzer）的关系是什么？

2. 三地址码（3-Address Code, 3AC）是什么，它的常用形式有哪些？

3. 如何在中间表示（Intermediate Representation, IR）的基础上构建基块（Basic Block, BB）？

4. 如何在基块的基础上构建控制流图（Control Flow Graph, CFG）?