# 7 指针分析-基础

# 7.1 指针分析的规则

在上一讲的最后，我们提到了Java中的 5 类指针影响型语句（见6.4.2）。在这一讲的前 3 大部分中，我们会重点聚焦于创建、赋值、存储、载入这四种，也就是说，我们会先从过程内分析开始做起；最后第 4 部分里面，我们会引入调用语句，学习全程序的指针分析。

# 7.1.1 定义和记号

为了后续的表示方便，我们先定义一些表示记号。

内容	记号
变量（Variables）	$x, y \in V$
字段（Fields）	$f,g \in F$
对象（Objects）	$o_i, o_j \in O$
实例字段（Instance Fields）	$o_i.f, o_j.g \in O\times F$

有了上述的记号之后，我们可以形式化的定义什么是指针，以及一个程序中指针的集合。

定义7.1

记某程序中的变量集合为 $V$ ，字段集合为 $F$ ，对象集合为 $O$ ，定义这个程序中的某个 指针（Pointer） 为 $p$ ，其中 $p$ 满足

p\in V\cup(O\times F)

记所有的指针组成的集合为 $Pointer$ ，则 $Pointer$ 满足

Pointer \subseteq V\cup(O\times F)

指针分析的目的是输出整个程序中所有的指向关系，根据上述定义，我们也可以形式化的定义出指向关系。

定义7.2

记程序的指针集为 $Pointer$ ，对象集合为 $O$ ，其幂集记为 $P(O)$ ，定义 指向关系（Points-to Relation） 是从 $Pointer$ 到 $P(O)$ 映射，用 $pt$ 表示，满足

pt \subseteq Pointer \times P(O)

于是，我们可以用 $pt(p)$ 来表示指针 $p$ 的 指向集合（Points-to Set） 。

# 7.1.2 规则

我们用推导式的方式来描述各种语句在指针分析中的规则。

定义7.3

考虑命题 $P_1, P_2, ... P_m$ 和命题 $Q_1, Q_2, ..., Q_n$ ，定义 推导式（Comprehension） 形式如下：

\frac{P_1, P_2, ..., P_m}{Q_1, Q_2, ..., Q_n}

其含义是，若 $P_1, P_2, ... P_m$ 为真，则 $Q_1, Q_2, ..., Q_n$ 为真。其中， $P_i$ 称为 前提（Premises） ， $Q_j$ 称为 结论（Conclusion） 。若 $m = 0$ ，则称结论 无条件（Unconditional） 成立。

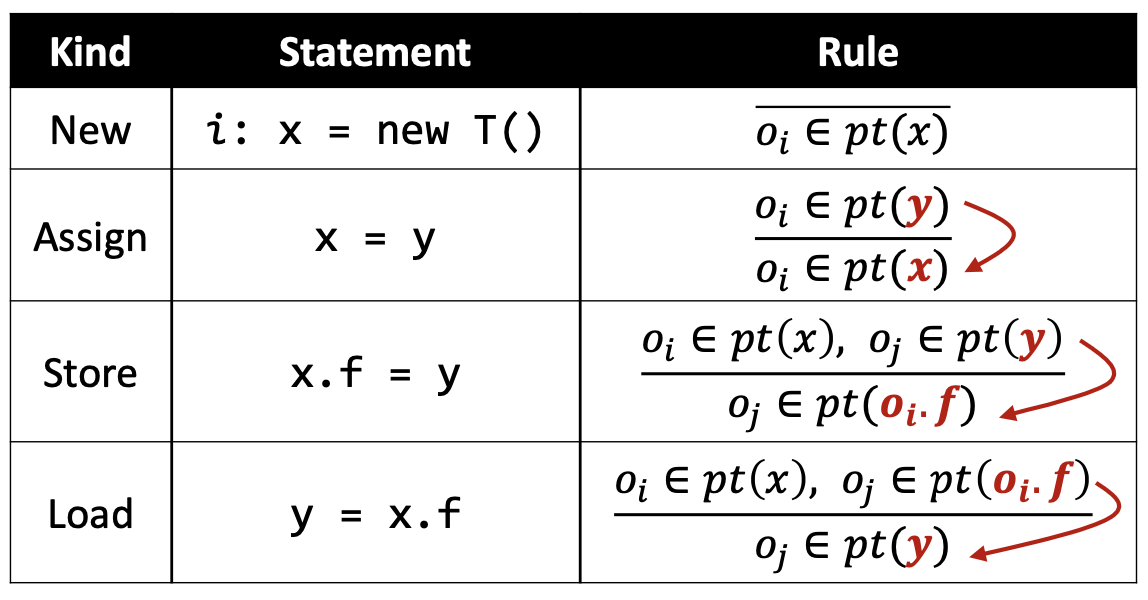
于是各种类型语句的规则可以用下表表示：

类型	语句	规则
创建	`i: x = new T()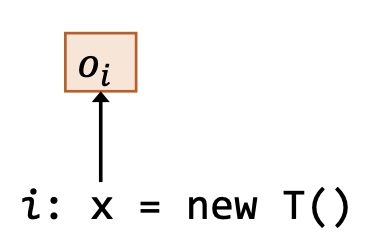`	$\overline{o_i \in pt(x)}$
赋值	`x = y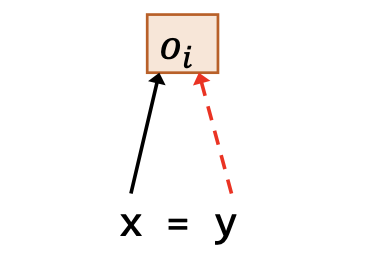`	$o_i\in pt(y)$ $\overline{o_i \in pt(x)}$
存储	`x.f = y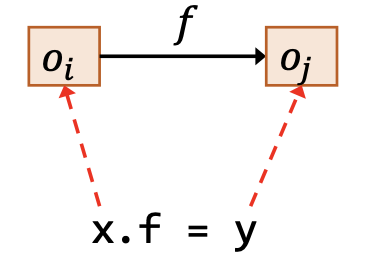`	$\underline{o_i \in pt(x), o_j\in pt(y)}$ $o_j \in pt(o_i.f)$
载入	`y = x.f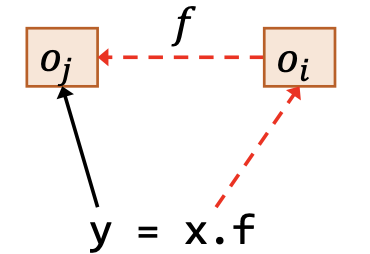`	$\underline{o_i\in pt(x), o_j\in pt(o_i.f)}$ $o_j\in pt(y)$

其中，图示用红色虚线表示作为前提的指向关系，用黑色实线表示结论得出的指向关系。

# 7.2 如何实现指针分析

# 7.2.1 实现思路

指针分析就是要在指针（变量或者实例字段）之间传播(propagate)指向信息。

propagate

定义7.4

我们根据语句的语义确定了一系列的指向集合传播规则，从而我们可以将指针分析的过程视为求解一个 包含约束(Inclusion Constraints) 系统的过程，这种分析风格被称为 安德森式分析（Andersen-Style Analysis） 。

实现指针分析的关键是当 $pt(x)$ 改变的时候，将改变的部分传递给和 $x$ 相关的其他指针。

因此，我们的解决方案是：

使用一个图来连接相关的指针；
当 $pt(x)$ 改变的时候，将改变的部分传递给 $x$ 的后继们。

# 7.2.2 指针流图

定义7.5

一个程序的 指针流图(Pointer Flow Graph) 指的是表示对象如何在程序中的指针之间流动的有向图。

PFG中的一个节点 $n$ 代表了一个变量或者某个对象的一个字段，即

n \in Pointer \subseteq V \cup (O\times F)

PFG中的一条边 $x \to y \in Pointer\times Pointer$ 表示指针 $x$ 指向的对象可能会流到指针 $y$ 的指向集合中（即也可能被 $y$ 指向）。

其中， $V$ 表示程序中所有变量的集合， $O$ 表示所有对象的集合， $F$ 表示所有字段的集合。

PFG的节点是容易确定的，就是程序中所有的指针；于是，我们只需要根据程序中的语句以及语句对应的规则添加PFG的边即可。

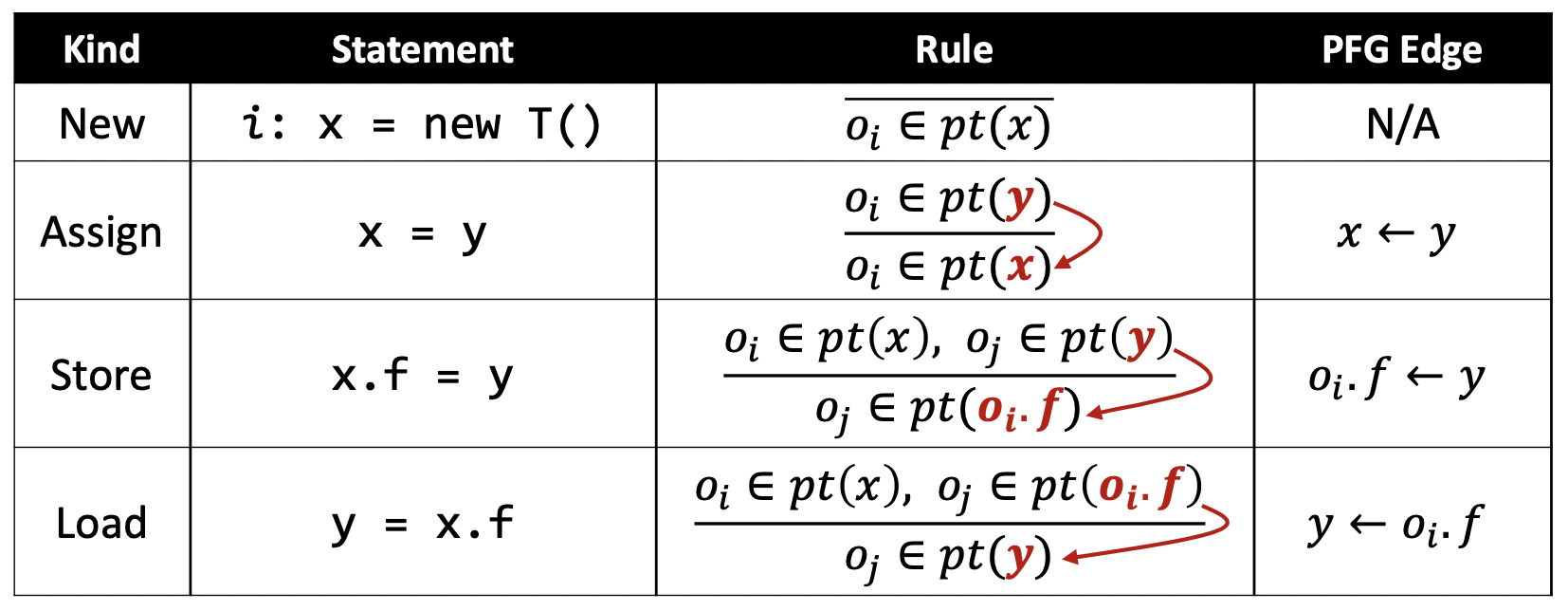
pfg-edges

比如说下面这个例子：

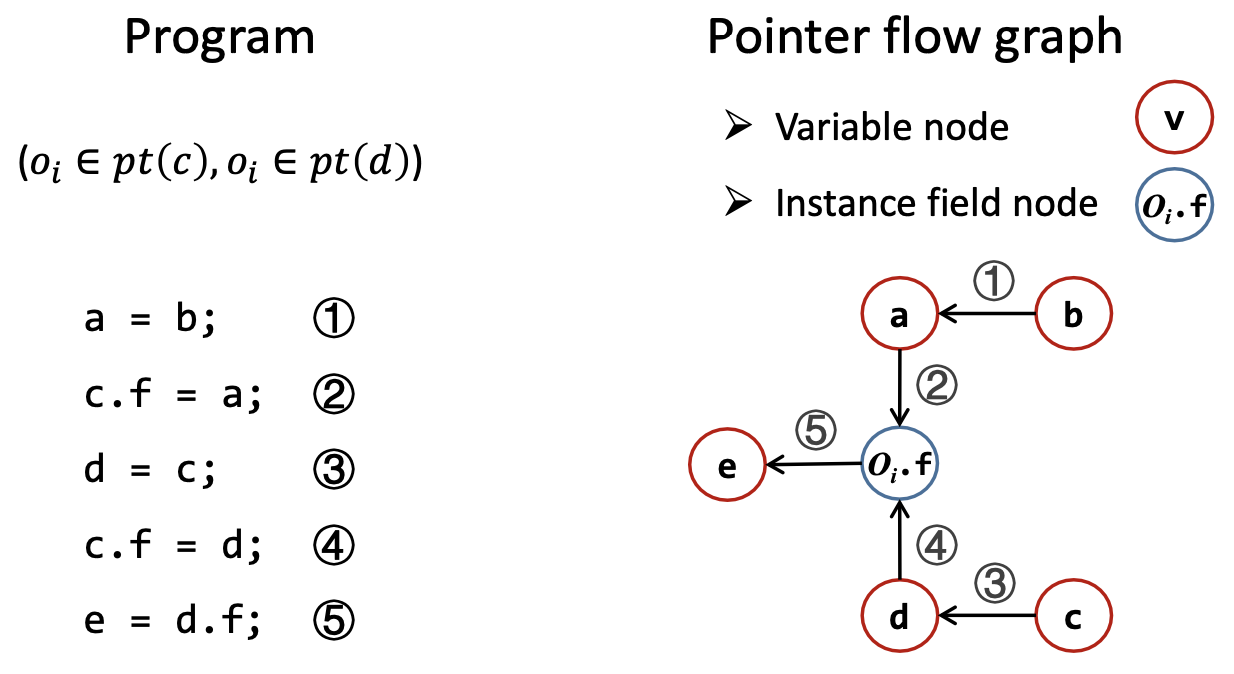
pfg-eg

有了PFG之后，指针分析就可以通过计算PFG的传递闭包（Transitive Closure）来解决。

比如说，在上面的例子中， $e$ 是从 $b$ 可达的结点，这就意味着所有的 $b$ 指向的对象都可能会流向 $e$ ，也就是可能还会被 $e$ 指向。

# 7.2.3 分析的步骤

如果程序中有这样一句语句： j: b = new T() ，显然有 $o_j \in pt(b)$ ，根据PFG，也会有 $o_j \in pt(a)$ ， $o_j \in pt(o_i.f)$ ， $o_j \in pt(e)$ 。

所以，指针分析的实现可以分两步：

构建指针流图 PFG
在 PFG 上传递指向信息

但是，上面这两步是没有严格的先后关系的。考虑存储语句和载入语句（即上面例子中的2、4、5行），一个指针是没有字段的，当我们通过指针来访问字段的时候，其实访问的是指针指向的对象的字段，也就是说，图中的2、4、5这3条边的构建就已经使用到了 $o_i \in pt(c)$ 和 $o_i \in pt(d)$ 这两条指向信息了。

因此，我们发现，构建指针流图是需要用到指向信息的，而传递指向信息又需要指针流图的基础，因此上面所说的两步是相互依赖（Mutually Dependent）的。

总结一下就是：

结论7.1

指针流图是在指针分析的过程当中 动态更新（Dynamically Updated） 的。

# 7.3 指针分析算法

# 7.3.1 算法内容

算法7.1 过程内上下文不敏感的全程序指针分析算法

# 7.3.2 算法分析

# 工作列表

工作列表（Worklist）包含了即将被处理的指向信息。

WL \subseteq Pointer \times P(O)

每个工作列表里面的表项 $(n, pts)$ 是一个指针 $n$ 和指向集合 $pts$ 的有序对，意味着 $pts$ 应当被传递给 $pt(n)$

$[(x, \{o_i\}), (y, \{o_j, o_k\}), (o_j.f, \{o_l\}), ...]$

# 处理 `New` 和 `Assign`

算法的第 8 - 13 行是对创建语句和赋值语句的处理。创建语句的规则是无条件的，所以它们是我们算法指向关系的初始状态。赋值语句是最简单的 PFG 边，在添加边的子过程中（算法第 31 - 38 行），我们主要做了 3 个步骤：

如果 $s\to t$ 已经在 PFG 中，则啥也不干，避免冗余操作（第 32 行）
添加 PFG 边（第 33 行）
保证每个 $s$ 指向的对象也被 $t$ 指向（第 34 - 36 行）

在算法的第 14 - 17 行是对于工作列表中的表项的处理，后面 18 - 27 行是对于 Store 和 Load 的处理，我们这里暂时不考虑。

对于工作列表中的每个表项，我们将其取出（第 15 行），然后取 $pts$ 中还不在 $pt(n)$ 里面的那部分对象集合（第 16 行），这是为了避免冗余的操作，然后通过子过程 $Propagate(n, \Delta)$ 将 $\Delta$ 传播给 $n$ 及其后继。

在第 40 - 47 行的传播子过程，我们主要干了下面 3 个步骤：

如果 $pts$ 是空集，则啥也不干，因为空集就没必要向后传播了（第 41 行）
将 $pts$ 传播给 $n$ 的指向集合 $pt(n)$ （第 42 行）
将 $pts$ 传播给 $n$ 在 PFG 上的后继结点（第 43 - 45 行）。

这里的 $pts$ 是在原来的指向集合基础上新增的对象集合，因为我们第 17 行传入的参数是 $\Delta$ 。

# 差量传播

定义7.6

称算法7.1第 16 - 17 行避免处理和传播冗余指向信息的做法为 差量传播（Differential Propagation） 。

使用差量传播的原因是算法的过程保证了现存于 $p(n)$ 中的指向信息已经被传播给 $n$ 的后继了，也就不需要再次被传播了。

实际上，和已有的指向集合相比， $\Delta$ 通常是很小的，所以仅仅传播新的指向信息 $\Delta$ 能够极大地提升效率。

除此之外， $\Delta$ 在处理存储、载入以及调用语句的时候对于效率的提升也很有作用，这些会在后续加以解释。

# 处理 `Store` 和 `Load`

在算法7.1的第 18 - 27 行，我们处理了 Store 和 Load 语句，这两种语句的指针流是会受已知的指向关系的影响的，新的指向关系可能会在这两种语句的作用下引入新的PFG边

因为我们是基于3地址码的IR讨论的指针分析，所以不存在实例域的嵌套访问，也就是说我们只会通过变量访问实例域（详见6.4.2），因此才有了第 18 行的判断，可以避免后续冗余的处理（如果 $n$ 是一个实例字段，则不会存在关于 $n$ 的 Store 和 Load 语句）。

具体的处理很简单，对于所有指向集中新增的对象，更新和这个变量相关 Store 和 Load 语句产生的PFG边。

一个 Assign 语句只会产生一个PFG边，而一个 Store 或者 Load 语句可能会产生多个PFG边。

# 7.3.3 实例

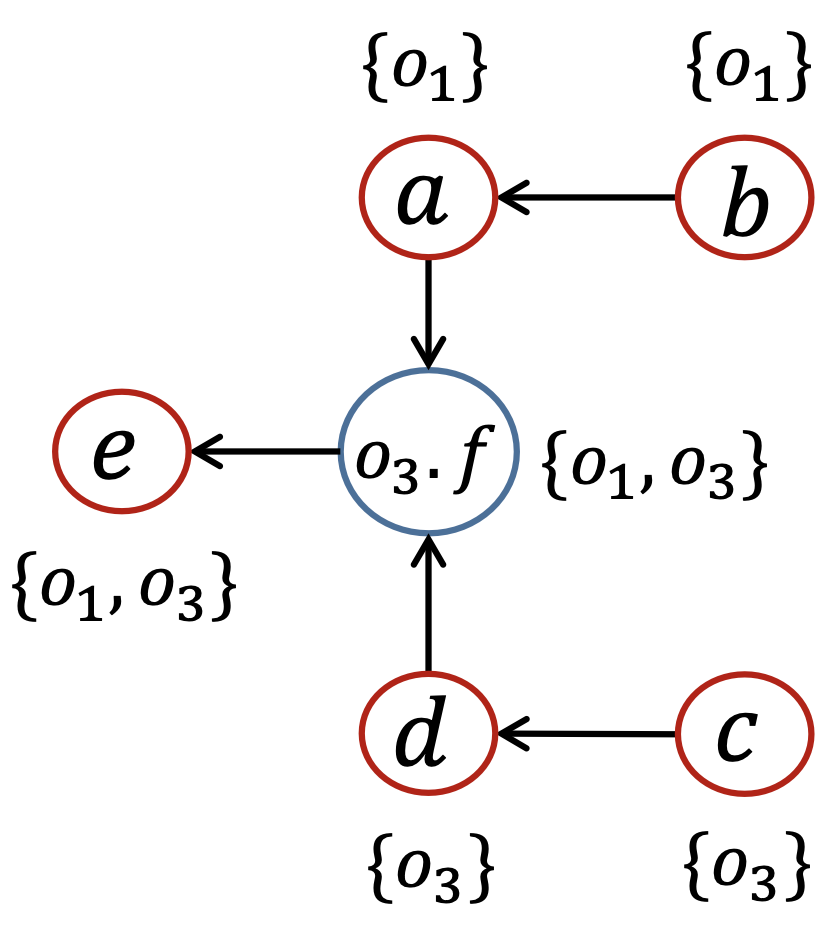
比如说下面这段程序：

b = new C();
a = b;
c = new C();
c.f = a;
d = c;
c.f = d;
e = d.f;

1
2
3
4
5
6
7

应用算法7.1，可以得到对应的PFG以及各指针结点的指向集合为：

pta-intra-alg-eg

# 7.4 带方法调用的指针分析

# 7.4.1 过程间分析与指针分析

过程间的指针分析需要调用图，我们之前调用图的构建方式是CHA，基于变量的声明类型来解析目标方法。不过这是极不精确的，因为CHA会引入很多虚假的调用边和指向关系。

而如果有了指针分析的话，我们就不必根据声明类型来解析目标方法，可以根据更精确的指向关系，即 $pt(x)$ 来解析目标方法了。而指针分析就会比CHA精确得多了，无论是在调用图构建还是在指向关系方面。

基于指针分析来构建调用图的过程中，反过来又会促进指针分析的过程，因为调用边和返回边也是会传递指向关系的，从而两者是相互依赖的，我们称这种调用图的构建方式为即时调用图构建（On-the-fly Call Graph Construction）。

定义7.7

称一边使用调用图，一边构建调用图的方式为即时调用图构建（On-the-fly Call Graph Construction）。

# 7.4.2 调用语句的规则

类型	语句	规则	PFG边
调用	`l: r = x.k(a1, ..., an)`	$o_i\in pt(x), m=Dispatch(o_i, k)$ $o_u\in pt(a_j), 1\le j\le n$ $o_v\in pt(m_{ret})$ $\overline{o_i\in pt(m_{this})}$ $o_u\in pt(m_{p_j}), 1\le j\le n$ $o_v\in pt(r)$	$a_1\to m_{p_1}$ ... ... $a_n\to m_{p_n}$ $m_{ret}\to r$

其中，

$Dispatch(o_i, k)$ 是根据对象 $o_i$ 的类型来做虚方法 $k$ 的派发（详见算法5.1），从而准确的找到对象 $o_i$ 对应的目标方法。这个方法派发是绝对精确的，因为Dispatch算法是对运行时的模拟。这里影响精度的因素只会是变量 $x$ 的指向集合内可能有不止一个指向对象。
$m_{this}$ 是 $m$ 方法对应的 $this$ 变量；
$m_{p_j}$ 是 $m$ 方法的第 $j$ 个形参；
$m_{ret}$ 是存放 $m$ 方法返回值的变量。

比如说下面的例子：我们会建立3条PFG边，并且将 $o_i$ 赋给 this 。

call-rule

这里需要再解释一下的问题是，我们为什么不添加 $x\to this$ 作为一条 PFG 边？

接收对象（Receiver Object）只应当流到对应目标方法的 this 变量中。比如说，如果 x 的指向集合里面有 T 类型的 $o_i$ ，以及 C 类型的 $o_j$ ，那么我们处理调用的时候，应当把 $o_i$ 赋给T类中的 foo 方法的 this 变量，把 $o_j$ 赋给 C 类中的 foo 方法的 this 变量。

如果我们在 x 和 this 之间建立了 PFG 边，那么 x 指向集中的所有对象都会流到 this 中，这会导致一个父类的对象流到子类的方法中，或者子类的对象流到父类的方法中（假设子类中存在目标实例方法），这是错误的，为 this 变量增加了虚假的指向关系，因此我们不添加 $x\to this$ 作为PFG边。

# 7.4.3 过程间的指针分析思路

过程间的指针分析是和调用图的构建一起进行的，也就是说，指针分析和调用图构建之间就像指针分析和指针流图构建之间一样，是相互依赖的。

调用图向我们描述了一个”可达的世界”：

入口方法（比如说 main 方法）是一开始就可达的；
其他的可达方法是在分析的过程中不断发现的；
只有可达的方法和语句才会被分析。

定义7.8

称调用图中，入口方法（Entry Methods）以及从入口方法可达的其他结点为可达方法（Reachable Methods）。所有的可达方法构成了一个可达调用子图（Reachable Sub-Call-Graph）。

其实我们平时所说的调用图，指的就是可达调用子图，对于控制流无法到达的其他方法，我们并不关心，也不必去分析。比如说我使用了一些库方法，这个库的类中有许许多多的方法，而我们不需要分析整个库，只需要分析我们的控制流可达的方法即可。

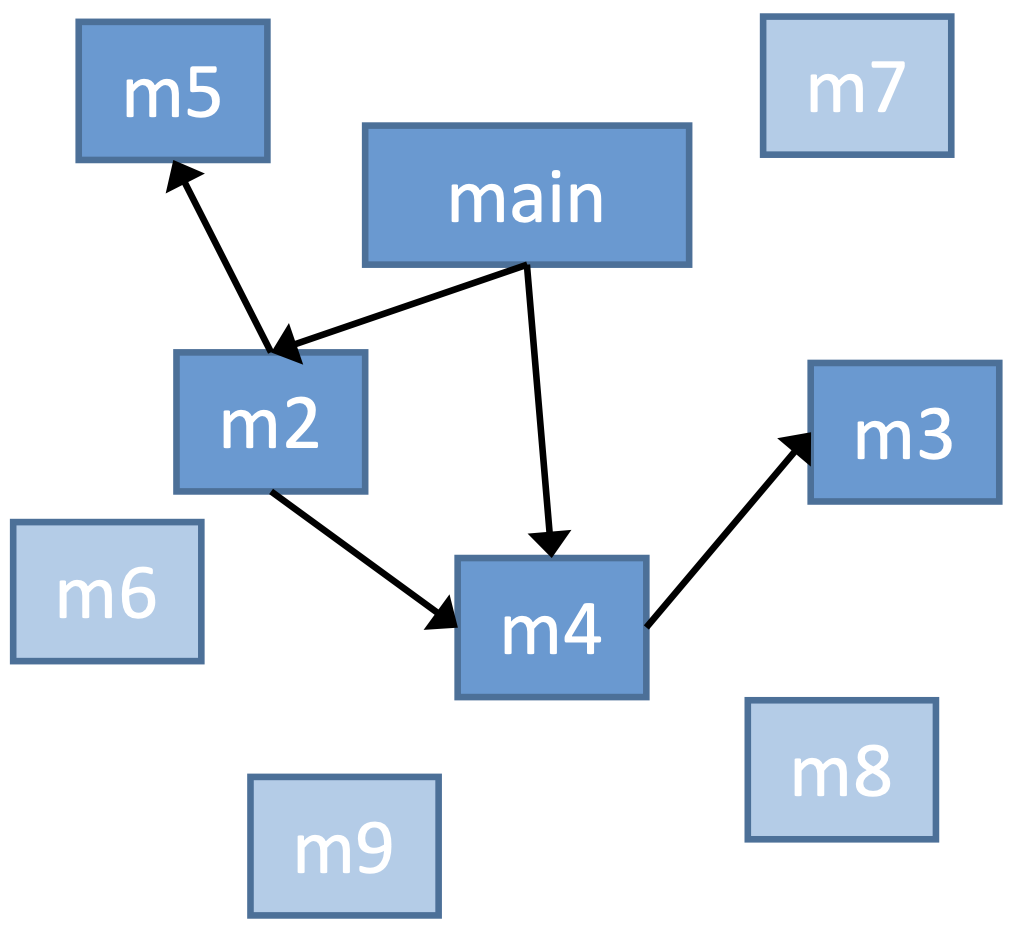
比如说下面这个例子， $m_6, m_7, m_8, m_9$ 就是不可达的方法，哪怕它们之间还有一些调用边之类的，我们也不关心了，因为程序的控制流不会经过那些边。

reachable

# 7.4.4 算法

# 算法内容

算法7.2 过程间上下文不敏感的全程序指针分析算法

其中， Propagate 和 AddEdge 子过程同算法7.1，Dispatch 过程见算法5.1。

# 算法分析

算法第 27 - 41 行的 AddReachable(m) 子过程是的作用是拓展可达调用子图，分为两步：

添加新的可达的方法和语句（算法第 28 - 30 行）
为新发现的语句更新工作表和指针流图（算法第 31 - 39 行）

这个子过程会在两种情况下被调用：

一开始的时候对入口方法调用（算法第8行）
当新的调用边被发现的时候对被发现的新方法调用（算法第 47 - 49 行）

这个算法中另一个新的子过程是算法 43 - 56 行的 ProcessCall(x, o_i) ，它的主要作用就是实现 7.4.2 中的调用规则，基本步骤为：

根据接收对象类型以及调用点处的方法签名作方法派发（第 44 - 45 行）
为目标方法的 $this$ 变量添加新的指向关系（第 46 行）
对新发现的目标方法即时（on-the-fly）构建调用图（第 47 - 49 行）
为新发现的目标方法建立传递参数和返回值的 PFG 边（第 50 - 53 行）

# 实例

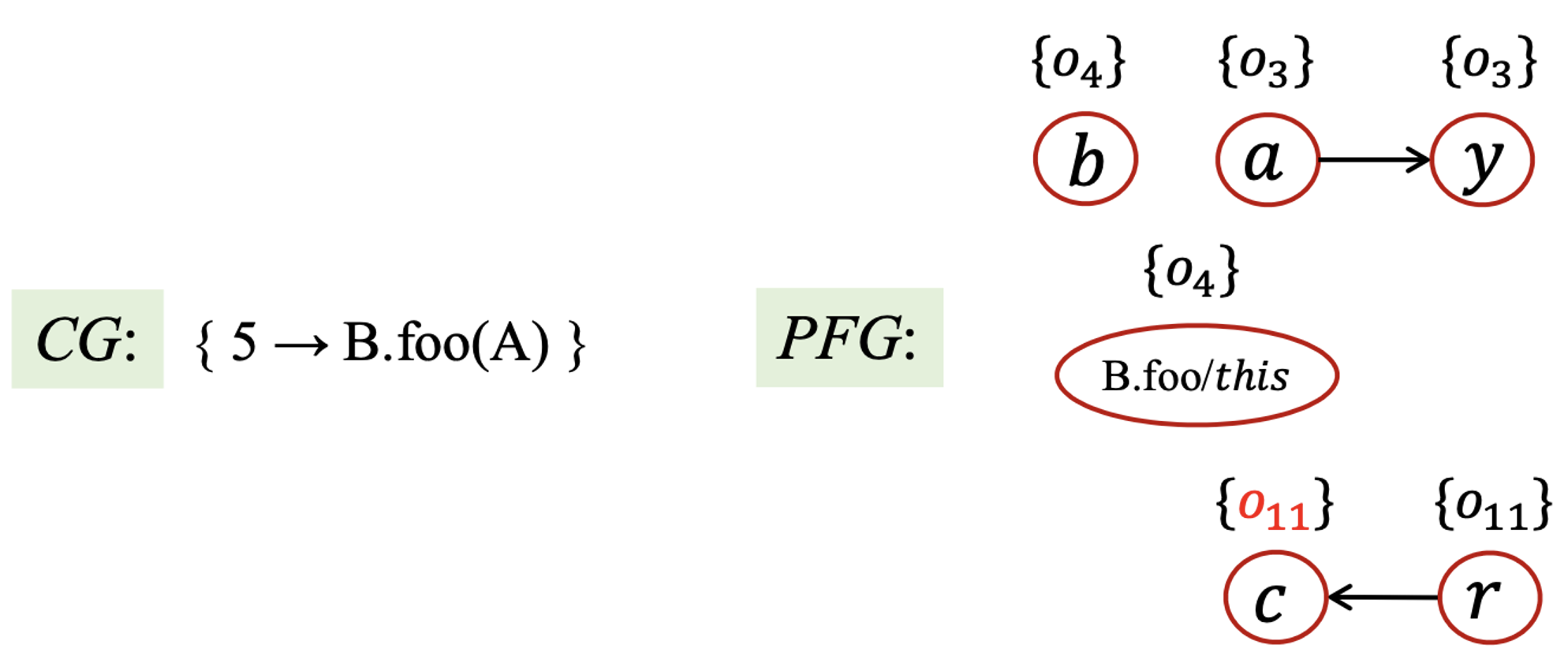
比如说，对于下面的一段程序：

class A {
    static void main() {
        A a = new A();
        A b = new B();
        A c = b.foo(a);
    }
    A foo(A x) {...}
}
class B extends A {
    A foo(A y) {
        A r = new A();
        return r;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14

运行算法7.2，我们可以得到如下的结果（读者可以自行尝试在纸上手动算一遍这个算法，能够加深印象）：

pta-inter-alg-eg

# 7.5 自检问题

指针分析的规则（Pointer Analysis Rules）是什么？
如何理解指针流图（Pointer Flow Graph）？
指针分析算法（Pointer Analysis Algorithms）的基本过程是什么？
如何理解方法调用（Method Call）中指针分析的规则？
怎样理解过程间的指针分析算法（Inter-procedural Pointer Analysis Algorithm）？
即时调用图构建（On-the-fly Call Graph Construction）的含义是什么？

作业布置

到此为止，读者已经具备了完成作业 5：非上下文敏感指针分析 (opens new window)所需的全部理论知识。

← 6 指针分析-引入 8 指针分析-上下文敏感 →